1. 双精度浮点数
干货
1. 通用知识
双精度浮点格式是计算机的一种数字格式,其全称为 double-precision floating-point format,也称 FP64 或 float64,它通常在内存中占 64 位,且使用浮动的小数点来表示较宽的数值范围。
双精度(double-precision):当单精度(32位)的范围或精度不够时,可以选择双精度(64位)
浮点(floating-point)用来表示分数或小数,或者当需要比相同位宽的定点提供更广范围的时候(即使以损失精度为代价)
在 IEEE 754-2008 标准中,64 位 base-2 格式被正式称为 binary64,它曾在 IEEE 754-1985 中被称为 double。IEEE 754 双精度二进制浮点格式,全称是 IEEE 754 double-precision binary floating-point format,即 binary64,通常也简称为 double。
IEEE 754 也指定了其它浮点格式,包括 32 位 base-2 单精度和近期的 base-10 表示。
最早提供单/双精度浮点数据类型的编程语言之一是 Fortran。在广泛采用 IEEE 754-1985 之前,浮点数据类型的表示和属性取决于计算机制造商、计算机模型以及编程语言的实现者(比如 GW-BASIC 的双精度数据类型是 64 位 MBF 浮点格式)。
2. 格式
2.1 binary64
IEEE 754 标准规定,binary64 的格式是:64 位 = 1 位符号 + 11 位指数 + 52 位有效数字。

符号位决定了数值本身的符号,详见 3.1 符号位
指数是偏差指数,需要考虑差值 1023,详见 2.2 偏差指数
有效数字的 52 位是显式存储的。除此之外,还有 1 个隐藏位,其值固定是 1,详见 3.2 有效数字的前导位约定
2.2 偏差指数
在 IEEE 754 浮点数中,指数在工程意义上是有偏差的,故称偏差指数,也称偏置指数。
之所以有偏差,是因为指数必须是“有符号”的值才能同时表示微小值和巨大值,但是二进制补码(通常表示有符号值)会让比较变得更加困难。为了解决这个问题,指数被存储为适合比较的“无符号值”,然后在解释的时候,加上偏差(存储时)或是减去偏差(读取时)就转成有符号范围内的指数了。
通俗地说,就是平移了下 x 轴,让能表示的所有数值都是非负数。比如长度固定是 4cm 的尺子,当 x=0 在其中间位置时,它能表示的数值范围是 [-2, 2];当 x=0 在其最左侧时,它能表示的数值范围是 [0, 4]。如下图:

偏差指数的原理也类似,就是在内存中存储的是红色的数据,等真正用时再转成绿色的数据。所以指数的实际值 = 内存中存储的值 - 差值。其中,差值为 2k−1−1,k 是指数的位数。
2 的 k-1 次方,之所以减 1 是相当于除以 2
2k−1-1,之所以减 1 是因为是从 0 开始计数的
比如:
单精度:指数有 8 位,差值就是 28−1−1=27−1=127
双精度:指数有 11 位,差值就是 211−1−1=210−1=1023
四精度:指数有 15 位,差值就是 215−1−1=214−1=16383
2.3 科学记数法
科学记数法是一种记数方法,其基数可以是 2、10 或者 16。
以基数是 10 的科学记数法为例,它与十进制表示法的对应关系如下:
0.00000000751
7.51∗10−9
0.2
2∗10−1
2
2
4321.768
4.321768∗103
8100000000
8.1∗109
当数字过大或者过小的时候,用十进制表示通常要写一长串数字,此时用科学记数法就比较方便了。科学家、数学家和工程师们通常使用十进制的科学记数法,部分原因就是它可以简化某些算术运算。
在十进制的科学记数法里,非零数字的写法是:a∗10n,其中 1≤|a|<10,n 是整数。
在计算机存储中,更常见的是二进制的科学记数法,即 a∗2n,其中 n 是整数,a 是由数字 0 和 1 以及小数点组成的二进制表示。示例如下:
0
0
0
1
1
1∗20
2
10
1.0∗21
3
11
1.1∗21
4
100
1.00∗22
5
101
1.01∗22
6
110
1.10∗22
7
111
1.11∗22
8
1000
1.000∗23
9
1001
1.001∗23
10
1010
1.010∗23
11
1011
1.011∗23
15
1111
1.111∗23
2.4 小结
至此,我们知道了给定的 64 位双精度浮点数在内存中的格式及其含义。
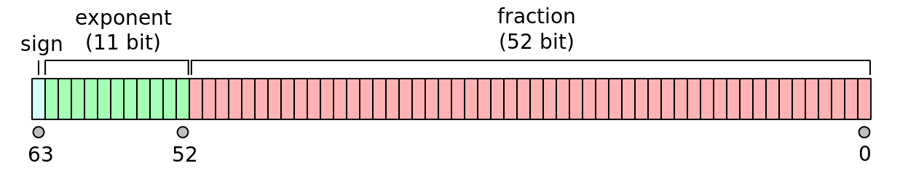
接下来,我们看看它在内存中的实际存储。
3. 内存存储
3.1 符号位
符号位比较直观,即−1sign。带入值就是:
当符号位值是 0 时,−10=1,数值是正数
当符号位值是 1 时,−11=−1,数值是负数
3.2 有效数字的前导位约定
值得一提的是,实际存储的有效数位是经过归一化或者规范化(normalization)处理的。
在二进制科学记数法里,非 0 数值的有效数首位必然是 1,所以在存储的时候就被省略了,只真正存储了小数点后面的数字部分。这个规则被称为前导位约定、隐式位约定、隐藏位约定或假定位约定。正因如此,52 位的有效数位能表示 53 位。
the leading bit convention,前导位约定
the implicit bit convention,隐式位约定
the hidden bit convention,隐藏位约定
the assumed bit convention,假定位约定
所以,IEEE 754 binary64 对应的真实数值就是:
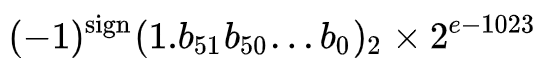
那么,对于数值 0 应该怎么存储呢?这种情况,除了和有效数位相关之外,还和指数位相关。
3.3 指数位编码
11 位指数是无符号整数,值从 0 到 2047。由于全 0 和全 1 的指数值是为特殊数字保留的,所以可用的指数值是从 1 到 2046。再减去指数偏差值 1023,就得到了指数的实际范围,是从 -1022 到 +1023。
00000000000(2)
保留值
±0 或次正规数
00000000001(2)
21−1023=2−1022
最小指数 emin
01111111111(2)
21023−1023=20
零偏移
11111111110(2)
22046−1023=2+1023
最大指数 emax
11111111111(2)
保留值
±Infinity 或 NaN
题外话,对于所有的 IEEE 754 格式,指数的最大值和最小值间都存在这样的关系 emin=1−emax。
3.3.1 指数全 0
当 11 位指数全是 0 的时候,即 e=00000000000(2)。此时看有效位的情况:
若 52 个有效位全是 0,则表示有符号的
±0若 52 个有效位不全是 0,则表示次正规数
当表示次正规时,会将有效数的前导位从 1 变成 0,然后实际指数按照指数的最小值 emin(即 -1022)来解释。这么做的目的是通过调整指数来去除有效数的前导 1,以此来表示比最小的正规数(相对次正规数而言)更接近 0 的数字。
次正规数能填补浮点运算中 0 附近的下溢间隙,从而避免“即使两个数值不相等,减法 a - b 也会下溢并产生 0”的情况(达到下溢时会丢弃所有有效数字,然后就突然变 0 了)。所以,次正规数有时也被称为逐渐下溢,因为它允许值非常小的计算结果慢慢地失去精度。次正规数可以保证浮点数的加减法永远不会下溢,两个相邻的浮点数总有一个可以表示的非零差。
在 IEEE 754-2008 中,非正规数(denormal numbers)被重命名为“次正规数”(subnormal numbers)。
3.3.2 指数全 1
当 11 位指数全是 1 的时候,即 e=11111111111(2)。此时看有效位的情况:
若 52 个有效位全是 0,则表示有符号的
±Infinity若 52 个有效位不全是 0,则表示
NaN
3.4 binary64 真实值

综上,IEEE 754 binary64 真实值的完整情况是:
当 e = 00000000000 且 f = 00...00 时,真实值是 (−1)sign∗0,即
±0当 e = 00000000000 且 f ≠ 00...00 时,真实值是 (−1)sign∗2emin∗0.fraction,即次正规数
当 e = 11111111111 且 f = 00...00 时,真实值是 (−1)sign∗Infinity,即
±Infinity当 e = 11111111111 且 f ≠ 00...00 时,真实值是
NaN其它情况,真实值才是 (−1)sign∗2e−1023∗1.fraction
其中,00...00 表示显式存储的 52 个有效位全是 0。
接下来,和大家一起感受下,十进制数值是如何以“双精度二进制浮点数”的格式存储在内存中的。
4. 实战
要想在计算机中存储十进制数值,需要:
将十进制转为二进制
整数部分:除 2 取余数(倒着取),直到商为 0
小数部分:乘 2 取整数(正着取),直到小数部分为 0
最后依据
符号(1位) + 指数(11位) + 有效数(52位)的格式,将值依次填充在 64-bit 中
以上步骤,我们用三个例子来实际感受下。
4.1 纯整数
以十进制数值 168 为例。
第一步,将十进制转为二进制。168(10)=10101000(2),逻辑如下:

第二步,将二进制写成科学记数法的形式。10101000(2)=1.0101000(2)∗27=1.0101(2)∗27,此时:
符号位是 0
指数是 7(未调整)
有效数是 1.0101(未标准化)
第三步,标准化有效数。1.0101 省略首位的 1 之后就变成了 0101。
第四步,调整指数,7+(211−1−1)=7+1023=1030。转成二进制是 1030(10)=10000000110(2),逻辑如下:

第五步,用 0 补齐指数(11 位)和有效数(52 位),最后再依次拼接即可。
符号位
0指数
100 0000 0110有效数
0101 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000

上图就是十进制数值 168 的 64 bits IEEE 754 格式。
4.2 纯小数
以十进制数值 0.125 为例。
第一步,将十进制转为二进制。0.125(10)=0.001(2),逻辑如下:

第二步,将二进制写成科学记数法的形式。0.001(2)=1(2)∗2−3,此时:
符号位是 0
指数是 -3(未调整)
有效数是 1(未标准化)
第三步,标准化有效数。1 省略首位的 1 之后就变成了 0。
第四步,调整指数。−3+(211−1−1)=−3+1023=1020,转成二进制就是 1020(10)=1111111100(2),逻辑如下:

第五步,用 0 补齐指数(11 位)和有效数(52 位),最后再依次拼接即可。
符号位
0指数
011 1111 1100有效数
0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000

上图就是十进制数值 0.125 的 64 bits IEEE 754 格式。
4.3 无限小数
这里指二进制世界里的无限小数,我们以十进制数值 0.1 为例。
第一步,将十进制转为二进制。0.1(10)=0.0001100110011...(2),逻辑如下:

此时,我们发现出现了循环(0011),用小数部分乘以 2 以后永远也不可能得到小数部分是 0 的情况。这个时候,就要进行四舍五入了。由于二进制只有 0 和 1,所以就 0 舍 1 入。这个就是计算机在存储小数时会出现误差的原因所在了,但因为保留的位数很多,精度较高,所以在大部分情况下误差可以忽略不计。
第二步,将二进制写成科学记数法的形式。0.0001100110011...(2)=1.100110011001...(2)∗2−4,此时:
符号位是 0
指数是 -4(未调整)
有效数是 1.1001 1001 1001 ...(未标准化)
第三步,标准化有效数。1.1001 1001 1001 ... 省略首位的 1 之后就变成了 1001 1001 1001 ...。
第四步,调整指数。−4+(211−1−1)=−4+1023=1019,转成二进制就是 1019(10)=1111111011(2),逻辑如下:

第五步,用 0 补齐指数(11 位)和有效数(52 位),最后再依次拼接即可。
符号位
0指数位
011 1111 1011有效位精度
1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1...因为有循环,所以最后一位要四舍五入(0 舍 1 入),最终结果是1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1010

上图就是十进制数值 0.1 的 64 bits IEEE 754 格式。
5. 总结
本文重点介绍了双精度二进制浮点数(即 binary64,也称 double)的格式及三个字段的含义。

需要特别注意的是,当它在存储小数的时候,可能会有精度损失(比如上方 0.1 的例子)。
只要是符合 IEEE 754 标准的(如 Fortran 里的 real64 类型、Java / C# / C / C++ 中的 double 类型、JavaScript 中的 Number 类型等),在存储小数的时候都有可能出现误差。这个在对精度要求比较高的场景下,是不能忽略的。常规的替代方案就是将小数转成整数(大数)进行存储和运算,最后显示的时候再恢复成小数形式。
6. 主要参考
补充两个在线小工具:
Last updated