4.2.1 入门动态规划

用状态图来分析问题

这部分从一个简单的例子出发，重点感受下借助状态图来分析和求解问题的思路。

题目：爬楼梯。每次可以爬 1 或 2 个台阶，现在有 n 个台阶，请问有多少种不同的走法？

两个思路：

1. 一步一步走（1 或 2 阶），直到走到 n 个台阶

2. 先走一步（1 或 2 阶），再走剩余的台阶，直到剩余 0

思路一

方案：依次确定每步

思路一是依次确定每一步该怎么走，如下：

• 第 1 步：可以走 [1] 或 [2]

• 第 2 步：可以走 [1] 或 [2]

• 第 3 步：可以走 [1] 或 [2]

• ...

• 第 i 步：可以走 [1] 或 [2]

• ...

• 直到走的台阶数达到 n 个。

以 n=7 为例，方案如下：

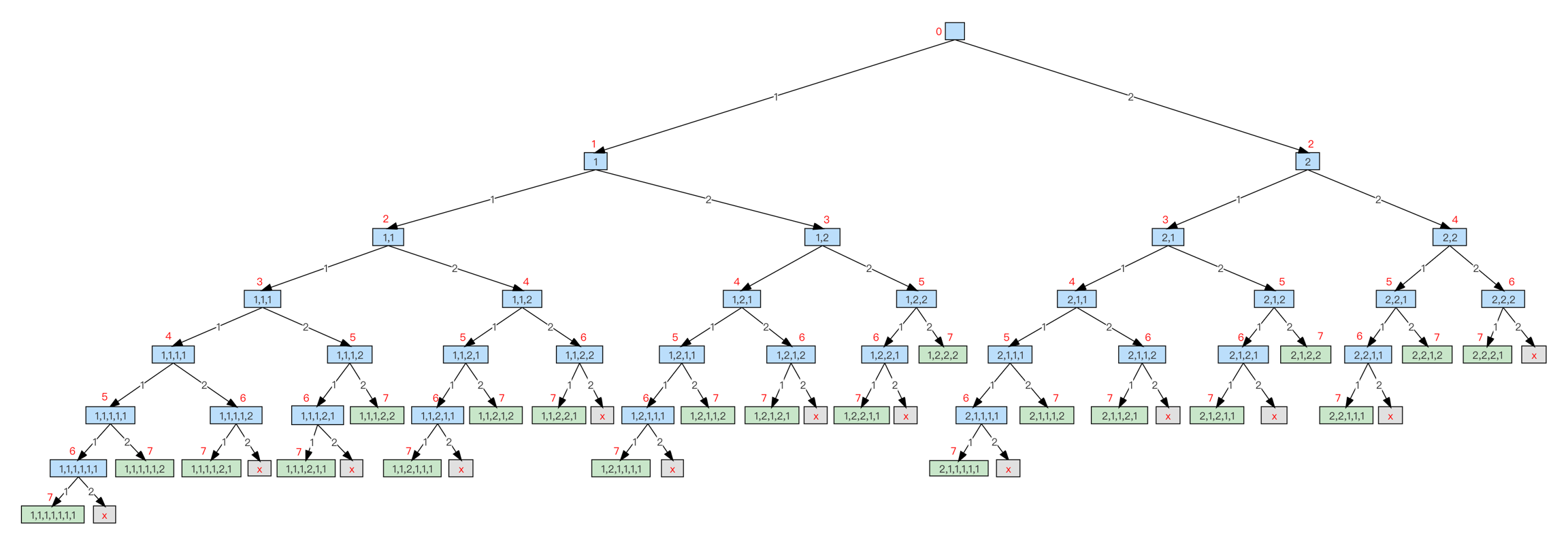
其中，蓝框里是具体的走法，红色数字表示当前走过的台阶总数，绿框是达到 n=7 这一目标了，是叶子结点。

这棵状态树，形式上和《4.1 递归》中介绍的排列模板类似——“依次考虑每个位置放哪个数字”，所以就直接写递归代码了，如下：

var climbStairs = function(n) {
  let ans = 0;
  // 递归：第i步怎么走
  let total = 0; // 当前走过的台阶总数（状态空间）
  const recur = function() {
    // 递归边界
    if (total > n) return; // 剪枝（跳过n的情况）
    if (total === n) {     // 若==n，则答案+1
      ans++;
      return;
    }
    // 本层逻辑
    // N叉树：可以走1，也可以走2
    for (let i = 1; i <= 2; i++) {
      total = total + i; // 走 
      recur();
      total = total - i; // 回溯
    }
  };
  // 开始递归
  recur();
  return ans;
};

运行结果：超出时间限制 最后执行的输入：44

很不幸，超时了。说明代码运行太慢了，来看看怎么优化。

优化：合并相同状态

这个思路是依次确定第 i 步怎么走，类似于“排列”。虽然是排列的思路，但代码里没记录具体的走法，只记录了当前走过的台阶总数，所以真实的状态图如下，其中蓝框和绿框里的数字就是“当前走过的台阶总数”。

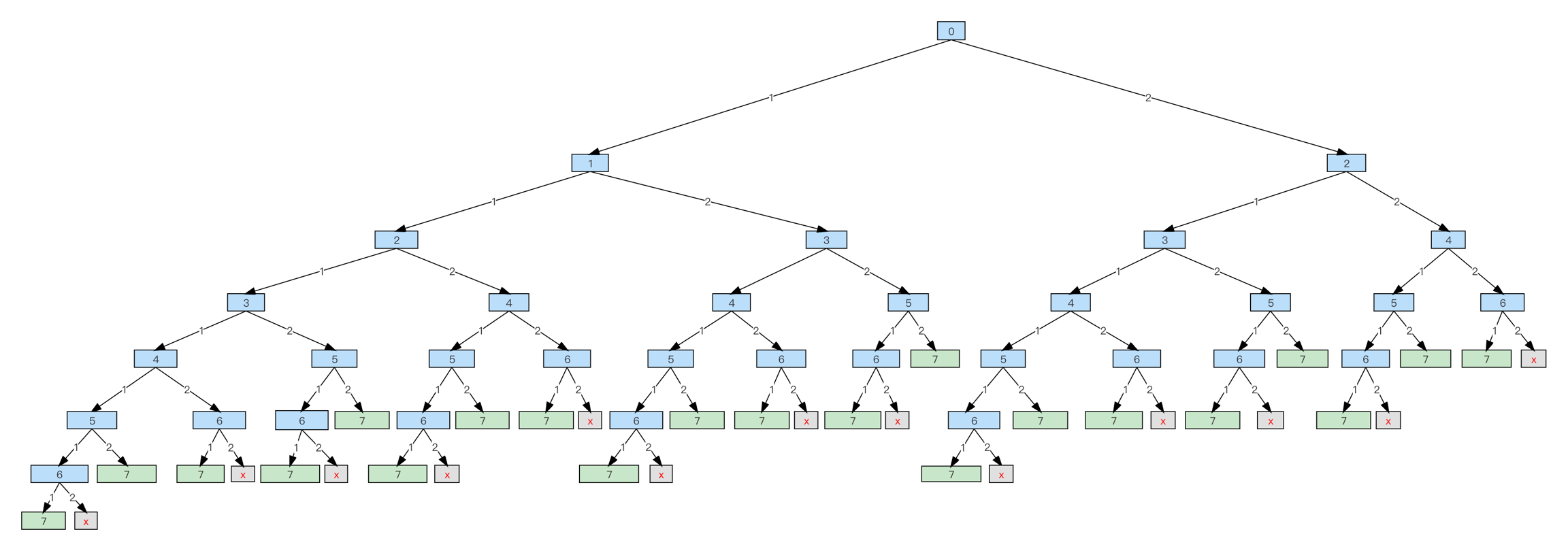
我们可以很直观地看到有很多重复的状态。将相同的状态合并了之后，状态图就从一棵树“变”成了一个有向无环图，其实说“变”是不合适的，因为树本来就是特殊的图。有向无环图如下：

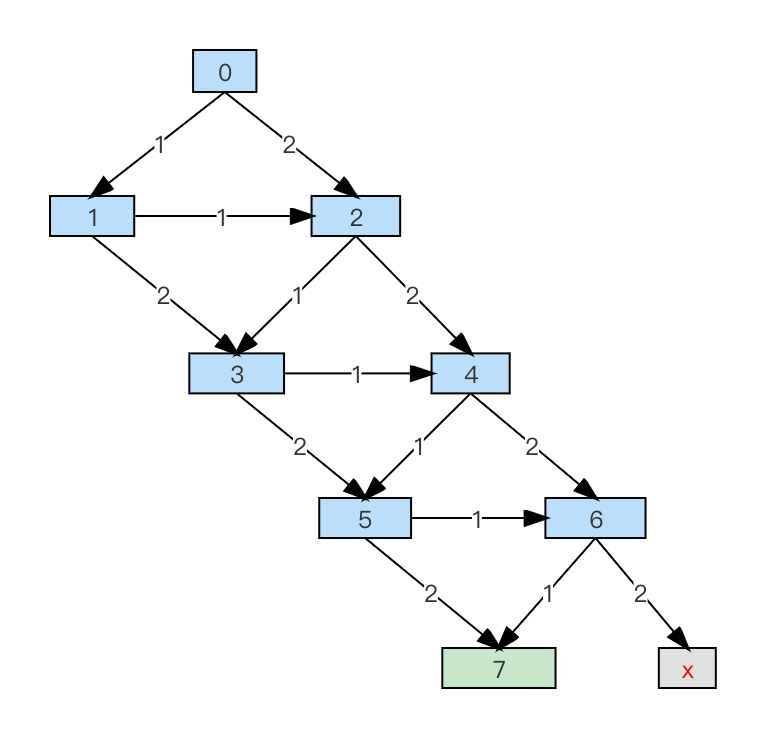
现在，我们试着遍历下这个有向无环图，思路依然是依次确定第 i 步怎么走。

广度优先遍历，代码如下：

var climbStairs = function(n) {
  // i个台阶，共有 steps[i] 种走法
  let steps = new Array(n + 1).fill(0);
  // 广度优先遍历：队列+入口
  const queue = [];
  queue.push(0);
  // 开始遍历，直到队列为空
  while (queue.length) {
    const front = queue.shift(); // 取队头
    steps[front]++; // 相应的走法+1
    // 如果台阶数==n，则找到一种
    if (front === n) continue;
    // 如果台阶数<n，则继续走
    else if (front < n) {
      queue.push(front + 1); // 再走1步（一条边让新结点入队）
      queue.push(front + 2); // 再走2步（一条边让新结点入队）
    }
  }
  return steps[n];
};

执行结果：超出时间限制 最后执行的输入：35

呃...依然超时，而且效果似乎更差了。为什么？

思考：状态树 vs 状态图

虽然相同的状态是被合并了，但是代码还是遍历了每条边每个点，因为该思路的本质是“排列”，排列的每一步都是独立且彼此依赖的，其整体才是最终答案。这就意味着即便是同一个结点，但因为达到它或是从它出发的边不同，致使它们依然是彼此不重叠的。

也就是说，这段广度优先遍历图的代码，和上面的深度优先遍历树的代码是一样的。代码之所以要遍历从 0-n 的每条路径，而没有使用布尔数组 visited[] 来避免相同结点的重复访问，就是因为它是通过统计具体的走法来计算总数的。

提问：题目里只要求计算有多少种走法，并没有要求列出每种走法的具体步骤，那么能否通过记录每个结点的“走法总数”，从而避免重复遍历图中的每个结点呢？

答案是肯定的，这其实就是我们的思路二。

思路二

方案：划分子问题

思路二是通过先走一步，从而将 n 阶的问题，划分成

• 先走 1 阶，再走 n-1 阶

• 先走 2 阶，再走 n-2 阶

这两个规模更小的子问题。其本质是分治。

继续以 n=7 为例，方案如下：

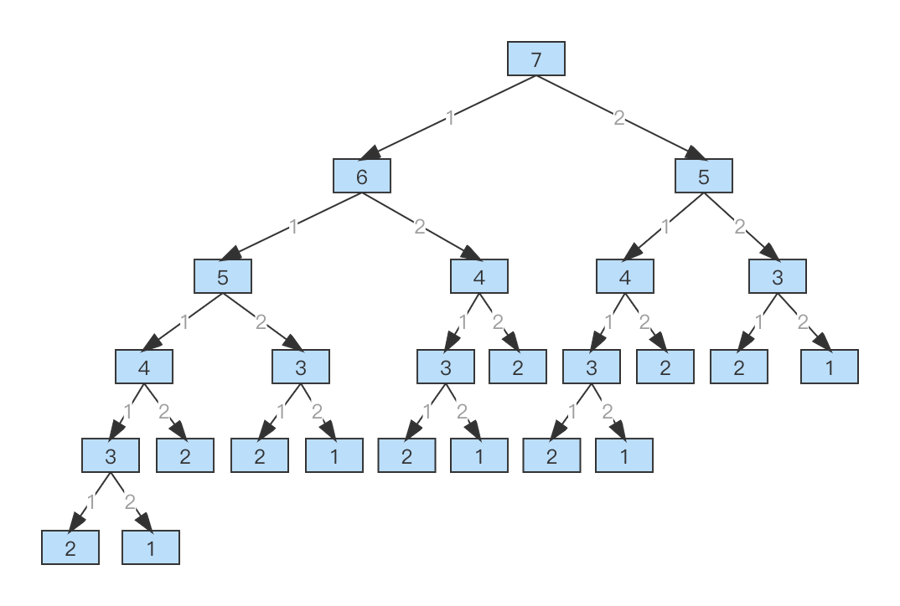
同样，将树中的相同状态合并下，就变成了一张图，如下：

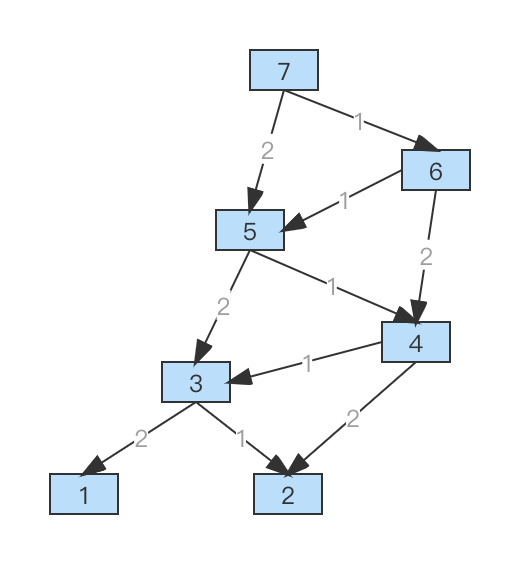
欸，合并后的图看起来和思路一的好像啊。这里我们对照着看下，下图中的左侧是思路二、右侧是思路一。它俩之所以看起来相似（一个倒着长一个正着长），是因为图里都隐藏了第二个状态，它们完整的状态都是个二元组，分别是 [台阶数, 走法总数]、[台阶数, 具体走法]。现在再从状态组的视角看它们，还是有本质不同的。

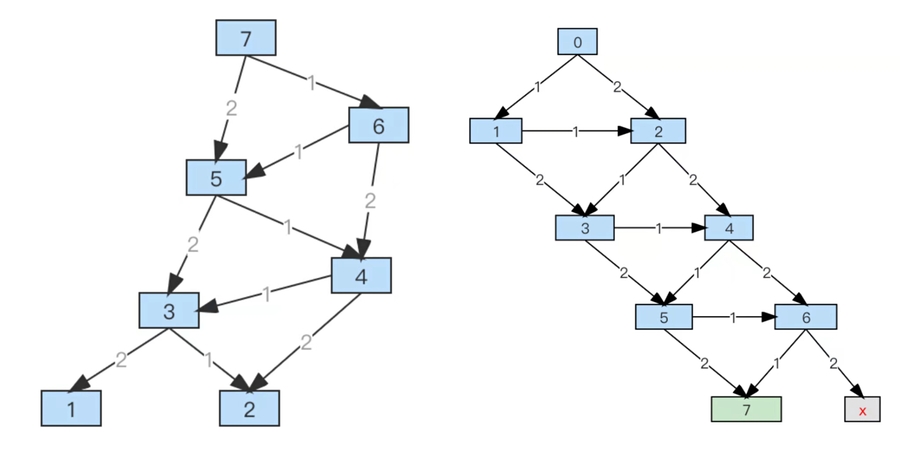
好，我们继续回到思路二（上图左一）。它是把 n 阶的问题划分成了 n-1 和 n-2 这两个子问题，如果用函数的形式 f(n) 表示 n 个台阶的走法总数，那么图中每个结点所对应的状态就是 [n, f(n)]，由它出发的两条边的含义就是 f(n) = f(n-1) + f(n-2)。

啊哈，这不就是斐波那契数列吗？那简单，递归实现，代码如下：

var climbStairs = function(n) {
  if (n === 1) return 1;
  if (n === 2) return 2; // [1,1], [2]
  return climbStairs(n - 1) + climbStairs(n - 2);
};

运行结果：超出时间限制 最后执行的输入：45

囧，还是超时。

通过打印 log，可以看到代码都递归了谁。继续以 n=7 为例，如下：

log: climbStairs(7)
log: climbStairs(6)
log: climbStairs(5)
log: climbStairs(4)
log: climbStairs(3)
log: climbStairs(2)
log: climbStairs(1)
log: climbStairs(2)
log: climbStairs(3)
log: climbStairs(2)
log: climbStairs(1)
log: climbStairs(4)
log: climbStairs(3)
log: climbStairs(2)
log: climbStairs(1)
log: climbStairs(2)
log: climbStairs(5)
log: climbStairs(4)
log: climbStairs(3)
log: climbStairs(2)
log: climbStairs(1)
log: climbStairs(2)
log: climbStairs(3)
log: climbStairs(2)
log: climbStairs(1)

我们发现递归了很多重复的 n，比如 n=5 两次，n=4 三次，n=3 五次，n=2 八次，n=1 五次。

优化：记忆化搜索

思考：能否把计算过的结果给存起来，等下次再递归到此 n 时就不用再继续向下探寻（递归）了？

当然可以。改造后的代码，如下：

var climbStairs = function(n) {
  // 存起来：当有 i 个台阶时，共有 cache[i] 种不同的走法
  const cache = [0, 1, 2];
  // 递归：深度优先遍历
  const dfs = function(i) {
    // 优先取缓存
    if (cache[i]) return cache[i]; // 1 <= n
    // 若没有，再向下探寻
    let p1 = cache[i - 1] ? cache[i - 1] : dfs(i - 1); // 同理，先取缓存
    let p2 = cache[i - 2] ? cache[i - 2] : dfs(i - 2); // 同理，先取缓存
    // 把结果存起来，再返回
    cache[i] = p1 + p2;
    return cache[i];
  };
  return dfs(n);
};

执行结果：通过

此时再运行 climbStairs(7)，递归的日志如下。计算的状态数明显少了，从指数阶 O(2n) 降到了线性阶 O(n)。

log: dfs(7)
log: dfs(6)
log: dfs(5)
log: dfs(4)
log: dfs(3)

这种将之前计算过的状态 [n, f(n)] 先存起来的解决方法，就是记忆化搜索，它能有效避免递归的重复下探，从而提高执行效率。大家是否有注意到，上述代码中用来存储状态的数据结构 cache[] 和我们遍历图时为了防止结点的重复访问而使用的布尔数组 visited[] 有异曲同工之妙，都是为了避免不必要的遍历（广度优先遍历的代码详见末尾的附录 B）。

优化：消除递归

还有一种可以有效避免递归重复下探的方法，那就是消除递归。对，就是不用递归实现了，改用 for 循环，代码如下：

var climbStairs = function(n) {
  // 存起来：当有 i 个台阶时，一共有 cache[i] 种不同的走法
  const cache = [0, 1, 2];
  // 开始迭代：从小到大
  for (let i = 3; i <= n; i++) {
    cache[i] = cache[i - 1] + cache[i - 2];
  }
  return cache[n];
};

从小到大的迭代，就天然地避免了状态的重复，因为它是纯纯的递推，而不像递归那样，先层层向下探寻（这步有可能出现“重复”），再层层向上递推。

你是否能想象的到，刚才写的 for 循环代码就是动态规划算法。

我们可以说把带记忆的递归搜索展开成 for 循环就是动态规划，也可以说记忆化搜索就是动态规划的递归实现，但它们都是表象。最根本的还是在于状态空间，就拿爬楼梯的例子来说，状态是个二元组 [n, f(n)]，状态转移方程是 f(n) = f(n-1) + f(n-2)。

记忆化搜索依托的是图，图中的结点对应的完整状态是 [n, f(n)]，图中的边的含义是 f(n) = f(n-1) + f(n-2)。而动态规划依托的是迭代——从小到大的迭代，至于如何确定迭代的递推公式，我们后面的文章会详细介绍。

总结

本文作为动态规划的入门，并没有对它进行过多的介绍，而是仅在末尾引出了动态规划。虽说如此，其实文章里的很多内容都和动态规划有着千丝万缕的联系。

比如我们常说，先暴力搜索，如果太慢就动态规划，如果还慢就贪心。那暴力搜索为什么慢？还记得上面的树形状态图吗？如下，树每长高一层就会多 2k 个状态，如果是 3 叉树或 4 叉树就会多 3k 或 4k 个状态。总之，状态空间是呈指数级增长的，诸如 2n, 3n ... 10n 等，这就是暴力搜索慢的根本原因。

即便是形态从树变成了图，依然可能是指数级增长的。还记得思路一（右）和思路二（左）的对比吗？只不过指数级增长从眼花缭乱的树结点个数，变成了图中边的个数的累乘。

状态图的“图”形结构也只是个表象，重点还是在于图中的边是如何迁移的、图中的结点是如何诠释该问题的。

暴力搜索想要升级成记忆化搜索，关键还是在于分治，即将原问题划分成“规模更小但解题思路一致”的子问题。只有在这样的状态空间里，才有可能（自然而然地）出现重叠的（子）状态，而它就是我们要记忆化的对象。

记忆化搜索本质上就是动态规划的递归实现。而我们常说的动态规划算法，大多数时候都是用 for 循环来实现的，因为它的代码更短小更简洁。正是因为它的简洁，以至于我们在代码里往往只看到了几层 for 循环和一个递推公式，就莫名其妙地把一个看起来还挺复杂的问题给解决了，其实它背后蕴藏着对状态空间的分析和改造。而本文的主要目的，就是学会借助状态图来分析和求解问题。

附录 A

最后的动态规划代码还可以进一步优化，将空间复杂度从 O(n) 降为 O(1)。代码如下：

var climbStairs = function(n) {
  let p1 = 0, p2 = 1;
  let ans = 0;
  for (let i = 1; i <= n; i++) {
    ans = p1 + p2;
    p1 = p2;
    p2 = ans;
  }
  return ans;
};

附录 B

记忆化搜索也可以用广度优先遍历实现，代码如下：

var climbStairs = function(n) {
  // 存起来：当有 i 个台阶时，共有 cache[i] 种不同的走法
  const cache = [0, 1, 2];
  // 广度优先遍历：队列+入口
  const queue = [];
  queue.push(3); // 从3个台阶开始
  // 开始遍历，直到队列为空
  while (queue.length) {
    const front = queue.shift();
    if (front > n) continue; // 如果台阶数>n，则忽略
    if (cache[front]) continue; // 如果该节点已访问，则忽略
    // 处理本层逻辑
    // 计算本台阶数的走法总数：要么从1步的台阶上来，要么从2步的台阶上来
    cache[front] = cache[front - 1] + cache[front - 2];
    // 将下个结点入队
    queue.push(front + 1);
    queue.push(front + 2);
  }
  return cache[n];
};